Arthur–Merlin protocol
In computational complexity theory, an Arthur–Merlin protocol is an interactive proof system in which the verifier's coin tosses are constrained to be public (i.e. known to the prover too). This notion was introduced by Babai (1985). Goldwasser & Sipser (1986) proved that all languages with interactive proofs of arbitrary length with private coins also have interactive proofs with public coins.
The basic assumption is that Arthur is a standard computer (or verifier) equipped with a random number generating device, while Merlin is effectively an oracle with infinite computational power (also known as a prover); but Merlin is not necessarily honest, so Arthur must analyze the information provided by Merlin in response to Arthur's queries and decide the problem itself. A problem is considered to be solvable by this protocol if whenever the answer is "yes", Merlin has some series of responses which will cause Arthur to accept at least 2/3 of the time, and if whenever the answer is "no", Arthur will never accept more than 1/3 of the time. Thus, Arthur acts as a BPP verifier, assuming it is allotted polynomial time to make its decisions and queries.
Contents |
MA
The simplest such protocol is the 1-message protocol where Merlin sends Arthur a message, and then Arthur decides whether to accept or not by running a probabilistic polynomial time computation. (This is similar to the verifier-based definition of NP, the only difference being that Arthur is allowed to use randomness here.) Merlin does not have access to Arthur's coin tosses in this protocol, since it is a single message protocol and Arthur tosses his coins only after receiving Merlin's message. This protocol is called MA. Informally, a language L is in MA if for all strings in the language, there is a polynomial sized proof that Merlin can send Arthur to convince him of this fact with high probability, and for all strings not in the language there is no proof that convinces Arthur with high probability.
Formally, the complexity class MA is the set of decision problems that can be decided in polynomial time by an Arthur–Merlin protocol where Merlin's only move precedes any computation by Arthur. In other words, a language L is in MA if there exists a polynomial-time deterministic Turing machine M and polynomials p, q such that for every input string x of length n = |x|,
- if x is in L, then
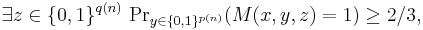
- if x is not in L, then
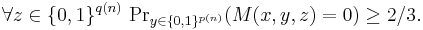
The second condition can alternately be written as
- if x is not in L, then
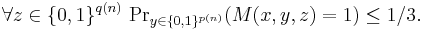
To compare this with the informal definition above, z is the alleged proof from Merlin (whose size is bounded by a polynomial) and y is the random string that Arthur uses, which is also polynomially bounded.
AM
The complexity class AM (or AM[2]) is the set of decision problems that can be decided in polynomial time by an Arthur–Merlin protocol with two messages. There is only one query/response pair: Arthur tosses some random coins and sends only the outcome of all his random coin tosses to Merlin, Merlin responds with a purported proof, and Arthur deterministically verifies the proof. In this protocol, Arthur is only allowed to send outcomes of coin tosses to Merlin, and in the final stage Arthur must decide whether to accept or reject using only his previously generated random coin flips and Merlin's message.
In other words, a language L is in AM if there exists a polynomial-time deterministic Turing machine M and polynomials p, q such that for every input string x of length n = |x|,
- if x is in L, then
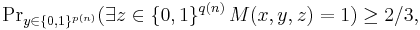
- if x is not in L, then
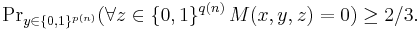
The second condition here can be rewritten as
- if x is not in L, then
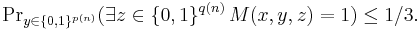
As above, z is the alleged proof from Merlin (whose size is bounded by a polynomial) and y is the random string that Arthur uses, which is also polynomially bounded.
The complexity class AM[k] is the set of problems that can be decided in polynomial time, with k queries and responses. AM as defined above is AM[2]. AM[3] would start with one message from Merlin to Arthur, then a message from Arthur to Merlin and then finally a message from Merlin to Arthur. The last message should always be from Merlin to Arthur, since it never helps for Arthur to send a message to Merlin before deciding his answer.
Properties
- Both MA and AM remain unchanged if their definitions are changed to require perfect completeness, which means that Arthur accepts with probability 1 (instead of 2/3) when x is in the language.[1]
- For any fixed k ≥ 2, the class AM[k] is equal to AM[2]. If k can vary polynomially on input size, the class AM[poly(n)] is a much stronger class, IP, which is known to be equal to PSPACE.
- MA is contained in AM, since AM[3] = AM, and Arthur can, after receiving Merlin's certificate, flip the required number of coins, send them to Merlin, and ignore the response.
- It is open whether AM and MA are different. Under plausible circuit lower bounds (similar to those implying P=BPP), they are both equal to NP.
- The conversion to a private coin protocol, in which Merlin cannot predict the outcome of Arthur's random decisions, will increase the number of rounds of interaction by at most 2 in the general case. So the private-coin version of AM is equal to the public-coin version.
- MA contains both NP and BPP. For BPP this is immediate, since Arthur can simply ignore Merlin and solve the problem directly; for NP, Merlin need only send Arthur a certificate, which Arthur can validate deterministically in polynomial time.
- Both MA and AM are contained in the polynomial hierarchy. In particular, MA is contained in the intersection of Σ2P and Π2P and AM is contained in Π2P. Even more, MA is contained in subclass SP
2 [2], a complexity class expressing "symmetric alternation". This is a generalization of Sipser–Lautemann theorem.
- AM is contained in NP/poly, the class of decision problems computable in non-deterministic polynomial time with a polynomial size advice. The proof is a variation of Adleman's theorem.
- MA is contained in PP; this result is due to Vereshchagin.
- MA is contained in its quantum version, QMA.
- AM contains the problem of deciding if two graphs are not isomorphic. The protocol using private coins is the following and can be transformed to a public coin protocol. Given two graphs G and H, Arthur randomly chooses one of them, and chooses a random permutation of its vertices, presenting the permuted graph I to Merlin. Merlin has to answer if I was created from G or H. If the graphs are nonisomorphic, Merlin will be able to answer with full certainty (by checking if I is isomorphic to G). However, if the graphs are isomorphic, it is both possible that G or H was used to create I, and equally likely. In this case, Merlin has no way to tell them apart and can convince Arthur with probability at most 1/2, and this can be amplified to 1/4 by repetition.
- If AM contains coNP then PH = AM. This is evidence that graph isomorphism is unlikely to be NP-complete, since it implies collapse of polynomial hierarchy.
- It is known, assuming ERH, that for any d the problem
-
- Given a collection of multivarariate polynomials
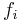each with integer coefficients and of degree at most d, do they have a common complex zero?
- Given a collection of multivarariate polynomials
- is in AM[3].
External links
Footnotes
- ^ For a proof, see Rafael Pass and Jean-Baptiste Jeannin (March 24, 2009). "Lecture 17: Arthur-Merlin games, Zero-knowledge proofs". http://www.cs.cornell.edu/courses/cs6810/2009sp/scribe/lecture17.pdf. Retrieved June 23, 2010.
- ^ Symmetric Alternation captures BPP
- ^ Madhu Sudan, Algebra and Computation lecture notes [1], lecture 22
References
- Babai, László (1985), "Trading group theory for randomness", STOC '85: Proceedings of the seventeenth annual ACM symposium on Theory of computing, ACM, pp. 421–429, ISBN 978-0-89791-151-1.
- Goldwasser, Shafi; Sipser, Michael (1986), "Private coins versus public coins in interactive proof systems", STOC '86: Proceedings of the eighteenth annual ACM symposium on Theory of computing, ACM, pp. 59–68, ISBN 978-0-89791-193-1.
- Arora, Sanjeev; Barak, Boaz (2009), Computational Complexity: A Modern Approach, Cambridge, ISBN 978-0-521-42426-4, http://www.cs.princeton.edu/theory/complexity/.
- Madhu Sudan's MIT course on advanced complexity
|
|||||||||||||||||